| Streak Lines as Tangent Curves of a Derived Vector Field | Corresponding Publication | |
 |
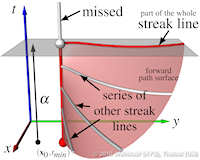
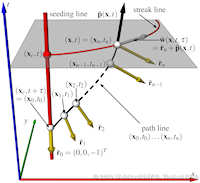
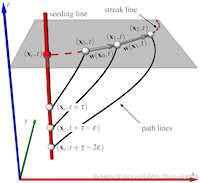
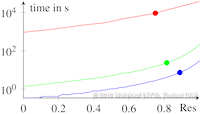
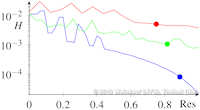
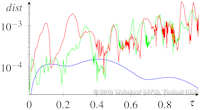
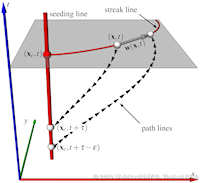
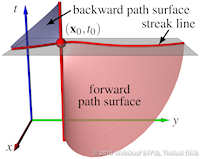
Characteristic curves of vector fields include stream, path, and streak lines. Stream and path lines can be obtained by a simple vector field integration of an autonomous ODE system, i.e., they can be described as tangent curves of a vector field. This facilitates their mathematical analysis including the extraction of core lines around which stream or path lines exhibit swirling motion, or the computation of their curvature for every point in the domain without actually integrating them. Such a description of streak lines is not yet available, which excludes them from most of the feature extraction and analysis tools that have been developed in our community. In this paper, we develop the first description of streak lines as tangent curves of a derived vector field - the streak line vector field - and show how it can be computed from the spatial and temporal gradients of the flow map, i.e., a dense path line integration is required. We demonstrate the high accuracy of our approach by comparing it to solutions where the ground truth is analytically known and to solutions where the ground truth has been obtained using the classic streak line computation. Furthermore, we apply a number of feature extraction and analysis tools to the new streak line vector field including the extraction of cores of swirling streak lines and the computation of streak line curvature fields. These first applications foreshadow the large variety of possible future research directions based on our new mathematical description of streak lines. | Streak Lines as Tangent Curves of a Derived Vector Field IEEE Transactions on Visualization and Computer Graphics (Proceedings Visualization 2010) 16(6), November - December 2010 Received the Vis 2010 Best Paper Award |
| [slideshow] | ||